穩態時
熱累積率零 δT/δt=0
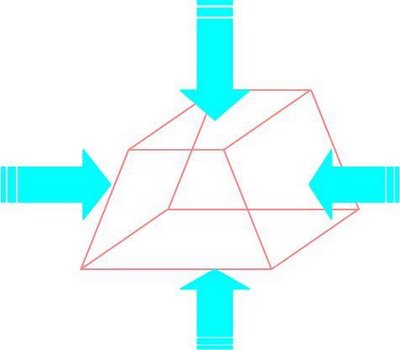
上述單位元素內,其熱對流熱傳導的總和即為熱累積量=0
所以由此可以建立下列平衡式:k{[t(i-1)+t(i)]/2 }{0.5*[R(i-1)+R(i)]}*(2π)}[T(i-1)–T(i)] / Δr+k{[t(I+1)+t(i)]/2 }{0.5*[R(i+1)+R(i)}*(2π)}[T(i+1)–T(i)] / Δr+2h(i)*2πr(i)Δr[Ta-T(i)] = 0
簡化
Ka=k*{[t(i-1)+t(i)]/2 };Kb=k*{[t(i+1)+t(i)]/2 }
原式可寫成
Ka[R(i-1)+R(i)]/Δr*[T(i-1)–T(i)]+Kb[R(i+1)+R(i)]/Δr*[T(i+1)–T(i)] +4h(i)r(i)Δr[Ta-T(i)]=0
再設 p(i)=Ka*[R(i-1)+R(i)]/Δr;
q(i)=Kb*[R(i+1)+R(i)]/Δr; s(i)=4*h(i)*R(i)*Δr
vpT(i-1)-(p+q+s)T(i)+qT(i+1)=-sTa i=2,3,…M-1
邊界條件

最內圈i=1,T(1)=To
最外圈i=M,多了最外環的熱流面
k{[t(M-1)+t(M)]/2 }{[R(M-1)+R(M)}/2*(2π)}[T(M-1)–T(M)] /Δr+
h(M)(2πR(M))*t(M)*[Ta-T(M)]+
2h(M)*{[R(M-1)+R(M)]/2+R(M)}/2*(2πΔr/2)*[Ta-T(M)] = 0
整理後
ss=p(M)+2h(M)R(M)t(M)+2h(M)[0.25R(M-1)+0.75R(M)]ΔrpT(M-1)-ssT(M) = -[ss-p(M)]*Ta
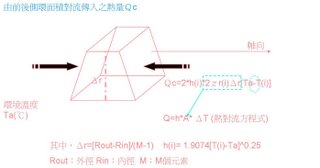
熱流量Qfin
R=Ri(最內圈)時,Qfin= - k(1) t(1)(2πR(1)[dT/dr]
因此從第一點流入第二點的熱流量為
Q=k(1) t(1)(2πR(1)[T1-T2]/Δr
熱對流時,與外界接觸的點溫度
Tm=[T1+Tr]/2=[T1+(T1+T2)/2]/2= (3/4)T1+(1/4)T2
Qfin=k(1) t(1)(2πR(1)[T(1)-T(2)]/Δr+ 2 (h(1)Δr/2){[(3/4)T(1) + (1/4)T(2)]-Ta}= k*t(1)*[T(1)-T(2)]/Δr + h(1)*[0.75T(1)+0.25T(2)-Ta]Δr
前置處理
n=hh(1);cc=hh(2);
mR=R/100;% length in cm
R1=mR(1);R2=mR(2);
thick=thick/1000;%
tt=linspace(thick(1),thick(2),M);%thickness at nodes
delR=(R2-R1)/(M-1);%length of each node
R=linspace(R1,R2,M);
A係數矩陣的建立
p=zeros(1,M);
q=p;s=p;T=p;T(1:M)=deal(To);
h(1:M)=deal(cc*To^0.25);(or n) h = 1.9074 (T- Ta)0.25
for i=2:M,p(i)=k*(tt(i-1)+tt(i))*(R(i-1)+R(i))/delR;endfor i=2:M-1,q(i)=k*(tt(i+1)+tt(i))*(R(i+1)+R(i))/delR;endT=T‘;h=h’; 行轉置成列
while 1h=cc*(T-Ta).^n;Tm=T(M);s=4*h.*R‘*delR;ss=p(M)+2*h(M)*R(M)*tt(M)+2*h(M)*(0.25*R(M-1)+0.75*R(M))*delR;C=[To -s(1:M-2)’*Ta -(ss-p(M))*Ta]‘;B=[0 0, q(2:M-1);1 -p(2:M-1)-q(2:M-1)-s(2:M-1)’ -ss;...p(2:M) 0]‘;A=spdiags(B,[1 0 -1],M,M);
帶狀對角矩陣以B為對角元素,[1 0 -1]為設定所在對角線位置
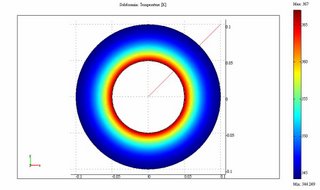
T=A\C;if abs(T(M)-Tm)<0.01,>使用FEMLAB模擬
執行結果與FEMLAB比較
續




No comments:
Post a Comment